Our diagram will consist of six dashed lines, numbered 1 through 6 from left to right. Summarizing this information gives the following schematic:

Now, we decide the most effective order for placing the elements on the diagram. Following the guidelines on page 31, we look for a condition that fixes the position of an element. There is none. Next, we look for a condition that limits the position of an element. The second condition, “Gori is the third person from the left,” limits Gori to spaces 3 and 4. This condition, as often happens with ordering games, generates two diagrams: one with the empty space to Gori's left and one with the empty space to his right:

Next, we look for a condition that connects two or more people. The last condition, BN, connects B with N. However, at this stage we cannot place it on the diagram. Finally, we look for a condition that states where a person cannot be standing. The first condition states that Chohan cannot be standing in space 1, 3, or 5. Noting this on the diagram yields
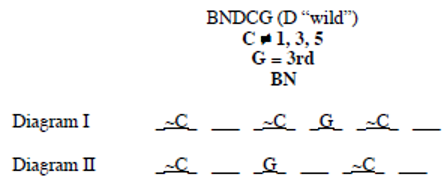
(Note: D is “wild” because the conditions do not refer to him. Thus D can stand in more positions than any other person.)
This diagram is self-contained. There is no need to refer to the original problem. If possible, always avoid rereading the problem. No further conditions can be derived, so we turn to the questions.
The structure of this question is awkward—the correct answer will always make a false statement! The question is more tractable when rephrased as “All of the following could be true EXCEPT.” Now, merely test each answer-choice against the initial conditions until you find the choice that violates one or more conditions.
Adding the supplementary condition, “space 6 is empty,” to the original diagrams gives
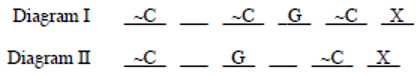
In Diagram I, the only space open for C is space 2:
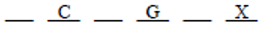
Clearly, this diagram does not leave room for the condition BN. So we eliminate Diagram I.
Next, test each answer-choice against Diagram II, starting with (A). Place Chohan in space 4 as follows:
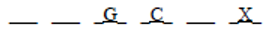
Now the condition BN forces B and N into spaces 1 and 2, respectively, which in turn forces D into space 5. So our uniquely determined diagram is
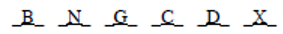
This diagram does not violate any initial condition. Hence Chohan could stand in space 4. So eliminate choice (A). Next, turning to choice (B), place Dani in space 4:
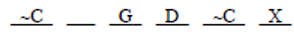
The condition BN forces B and N into spaces 1 and 2, respectively:
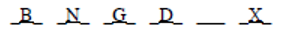
But this diagram forces C into space 5, violating the condition C ≠ 1, 3, 5. Hence D cannot stand in space 4, and the answer is (B).