The conditions “J and J are holding hands” and “L and L are holding hands” are naturally symbolized as JJ and LL, respectively. The condition “K and K are not holding hands” can be symbolized as K...K. [The symbol ~(KK) would also work well, but the symbol K...K is more descriptive because it shows the space between the Ks.] The condition “One of the Ls is at one end of the line, and one of the Ms is at the other end” can be symbolized as L=1st/last and M=1st/last. The diagram will consist of eight dashed lines numbered 1 through 8, from left to right:
JJ
LL
K ... K
L = First / Last
M = First / Last
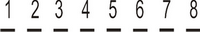
No significant conditions can be derived from the given information, and no conditions can be placed on the diagram. So we attack the questions.
This question requires an indirect proof. That is, take a sub-statement; then try to construct a valid diagram for it. If this cannot be done, it is an answer—otherwise it is not.
Start with Statement I. If M is in position 5, then, from the supplemental condition “M is in position 8” and the condition L=1st/last, we know that the Ls must be in positions 1 and 2:
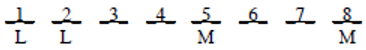
Now, the condition JJ forces the Js into either positions 3 and 4, or 6 and 7:

In both diagrams the Ks are forced next to each other, which violates the condition K...K. Hence Statement I cannot be true. This eliminates (B), (C), and (D), as they don’t contain I.
Next, Statement II is time consuming because we will have to check all three positions for the Ks. So skip to statement III. Place J in position 3:
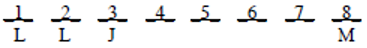
Then from the condition JJ, we know that the other J must be in position 4:
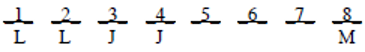
Then the Ks can be placed in positions 5 and 7 and the M in position 6—all without violating any conditions:
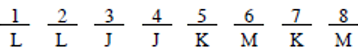
This is a valid diagram with J in position 3. Hence Statement III can be true. This eliminates (E). Therefore, by process of elimination, we have learned that the answer is (A), without having to check Statement II.